
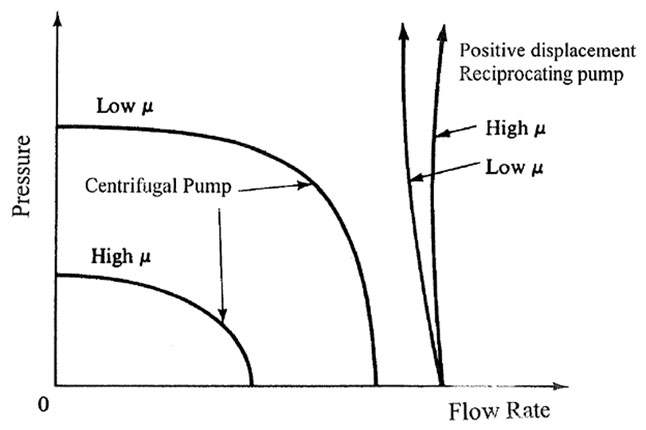
#COMPRESSOR PERFORMANCE CURVES PDF SOFTWARE#
The heart of any commercial process flow simulation software is an equation of state. For general planning purposes the graphical solutions shown in reference produce results comparable to these equations. The power calculation should be made per stage of compression and then summed for all stages connected to a single driver. The practical choice depends on the available data, although it is somewhat arbitrary. Equations 1 and 2 are equally correct theoretically. Where η and η P are the isentropic (or adiabatic) and polytropic efficiency, respectively, P 1 suction pressure, P 2 discharge pressure, T 1 and T 2 arethe suction and discharge temperatures, respectively, q is gas volume flow rate at standard condition of P S and T S, Z a average gas compressibility factor, k heat capacity ratio, R the gas constant, and n is the polytropic path exponent. The actual discharge temperature based on the polytropic is calculated by equation 4B.
The actual discharge temperature based on the isentropic path is calculated by equation 4A. Similarly, the polytropic head is calculated by equation 3B: The isentropic head is calculated by equation 3A: The isothermal process, however, is seldom used as a basis because the normal industrial compression process is not even approximately carried out at constant temperature.įor an isentropic (reversible and adiabatic) process, equation 1 can be written as:

Any one of these processes can be used suitably as a basis for evaluating compression power requirements by either hand or computer calculation. In the compression process there are three ideal processes that can be visualized: 1) an isothermal process, 2) an isentropic process and 3) a polytropic process. The results of a reversible process are then adapted to the real world through the use of an efficiency. Normally, the thermodynamic calculations are performed for an ideal (reversible process). Reference emphasizes that using a single value for each variable is not the correct way to evaluate a compression system. Thus the most difficult part of a compressor calculation is specification of a reasonable range for each variable and not the calculation itself. A compressor is going to operate under varying values of the variables affecting its performance. Gas composition is important but a small error here is less important providing it does not involve the erroneous exclusion of corrosive components. Where mass flow rate and h is specific enthalpy.įrom a calculation viewpoint alone, the power calculation is particularly sensitive to the specification of flow rate, inlet temperature and pressure, and outlet pressure. The theoretical power requirements are independent of compressor type the actual power requirements vary with the compressor efficiency. The results indicate that the accuracy of the shortcut method is sensitive to the value of heat capacity ratio, k.
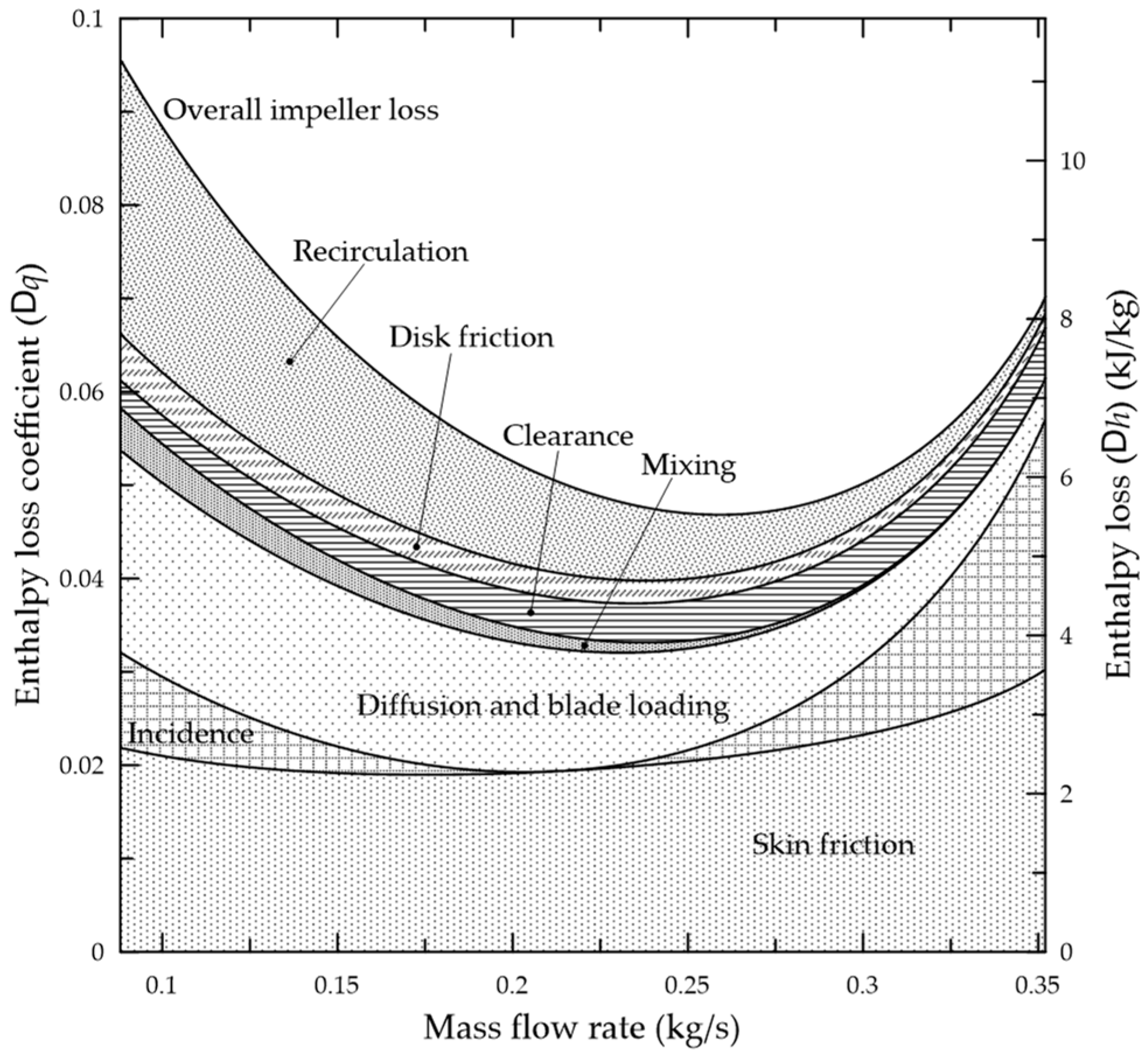
The enthalpies and entropies are used to determine the power requirement and the discharge temperatures. The rigorous method is based on an equation of state like the Soave-Redlich-Kwong (SRK) for calculating the required enthalpies and entropies. We will compare the rigorous method results with the values from the short cut methods. In this tip of the month (TOTM) we will present the compressor calculations of a case study.


 0 kommentar(er)
0 kommentar(er)
